مەزندەی گۆڵدباخ
مەزندەی گۆڵدباخ (بە ئینگلیزی: Goldbach's conjecture) لە تیۆریی ژمارەکان و بە گشتی لە بیرکاریدا، یەکێکە لە کۆنترین کێشەکانی بیرکاری کە شی نەکراوەتەوە و نەسەلمێندراوە، بە پێی ئەم مەزندەیە: «ھەر ژمارەیەکی تەواوی جووتی گەورەتر لە ٢ دەتوانرێت بە شێوەی سەرجەمی دوو ژمارەی سەرەتایی بنووسرێت.» بۆ نموونە:
- ٦ = ٣ + ٣
- ٨ = ٣ + ٥
- ١٠ = ٣ + ٧ = ٥ + ٥
- ١٢ = ٧ + ٥
- ...
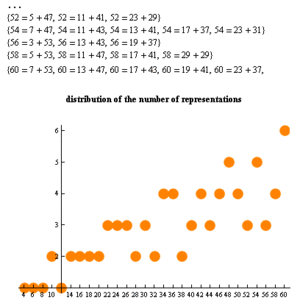
- ١٠٠ = ٣ + ٩٧ = ١١ + ٨٩ = ١٧ + ٨٣ = ٢٩ + ٧١ = ٤١ + ٥٩ = ٤٧ + ٥٣
- ...
کریستیەن گۆڵدباخ لە ساڵی ١٧٤٢ی زایینی لە نامەیەکدا کە بۆ لیۆنارد ئۆیلەری ناردووە باسی لێ کردووە. ئەم مەزندەیە لە سەرەتادا بەم شێوە بووە «ھەر ژمارەیەکی گەورەتر لە ٢، دەتوانرێت بە شێوەی سەرجەمی سێ ژمارەی سەرەتایی بنووسرێت.» بەپێی توێژینەوەیەک لە ساڵی ٢٠١٤دا وا دەرکەوتووە مەزندەی گۆڵدباخ بۆ ھەموو ژمارە جووتەکانی بچووکتر لە ٤ × ١٠١٨ ڕاستە.[٢]
کورتەمێژوو
[دەستکاری]![[icon]](/wiki/%D9%BE%DB%95%DA%95%DA%AF%DB%95:Wiki_letter_w_cropped.svg){kind=small} | ئەم بەشە واڵایە. دەتوانیت بە زیادکردنی یارمەتیی بدەیت. |
ھەوڵەکان بۆ سەلماندنی مەزندەی گۆڵدباخ
[دەستکاری]
لە ساڵی ١٩٦٦دا چن جینگ ڕان ماتماتیکزانی چینی توانی بسەلمێنیت ھەر ژمارەیەکی جووتی سەربەزیا گەورە دەتوانرێت بە شێوەی سەرجەمی ژمارەیەکی سەرەتایی و ژمارەیەکی تر کە یەکسانە بە ئەنجامی لێکدانی دوو ژمارەی سەرەتایی بنووسرێت. ھەروەھا لە ساڵی ١٩٩٥دا ئۆلیوێر ڕامار ماتماتیکزانی فەڕانسەوی سەلماندی ھەر ژمارەیەکی جووتی گەورەتر یان یەکسان بە ٤ دەتوانرێت بە شێوەی سەرجەمی شەش ژمارەی سەرەتایی بنووسرێت. لە ساڵی ١٩٣١دا ئیشنیرلمان (١٩٠٥–١٩٣٨) کە لەو سەردەمەدا ماتماتیکزانێکی لاو و نەناسراو بوو سەرکەوتنێکی گرینگی بەدەست ھێنا کە بۆ ھەموو پسپۆڕەکان چاوەڕواننەکراو و سەرنجڕاکێش بوو. ئیشنیرلمان سەلماندی ھەر ژمارەیەکی تەواوی ئەرێنی دەتوانرێت بە شێوەی سەرجەمی بەلایەنی زۆر ٣٠٠٠ ژمارەی سەرەتایی بنووسرێت. ھەرچەند ئەگەر ئەو ئەنجامە بەراورد بکرێت لەگەڵ ئامانجی سەرەکی واتە سەلماندنی مەزندەی گۆڵدباخ، ڕەنگە موزحیک و پێکەنیناوی بێت. بەڵام ئەوە بە یەکەم ھەنگاو دادەنرێت بۆ سەلماندنی مەزندەی گۆڵدباخ.
پەراوێزەکان
[دەستکاری]- ^ "Goldbach's Conjecture" by Hector Zenil, Wolfram Demonstrations Project, 2007.
- ^ Silva، Tomás Oliveira e. «Goldbach conjecture verification». www.ieeta.pt.
- ^ Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle (Band 1), St.-Pétersbourg 1843, pp. 125–129
سەرچاوەکان
[دەستکاری]- بەشداربووانی ویکیپیدیا، «حدس گلدباخ»، ویکیپیدیای فارسی. سەردان لە ٢٢ی ئەیلوولی ٢٠١٨.
 | ئەم «ماتماتیک» وتارە کۆلکەیەکە. دەتوانیت بە فراوانکردنی یارمەتیی ویکیپیدیا بدەیت. |
 |
کۆمنزی ویکیمیدیا، میدیای پەیوەندیدار بە مەزندەی گۆڵدباخ تێدایە. |