تێسێرەکت
لە ئەندازەدا، تێسێرەکت بە ھاوتای چوار ڕەھەندیی شەشپاڵوو دەوترێت، بە دەستەواژەیەکی تر تێسێرەکت بەرزەشەشپاڵوویەکی چوارڕەھەندییە.
دروستکردنی تێسێرەکت
[دەستکاری]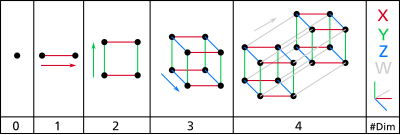
گریمان خاڵێکمان ھەبێت، خاڵ ھیچ ڕەھەندی نییە. ئەم خاڵە لە ئاڕاستەیەکدا ڕادەکێشین. ھێڵێک دروست دەبێت، ھێڵ تەنھا یەک ڕەھەندی ھەیە ئەویش درێژییە. ھێڵێک لە ناکۆتا خاڵ پێکدێت. ئینجا ئەم ھێڵە دەبەین بۆ بۆشایی دوو ڕەھەندی. بە ڕاکێشانی ئەم ھێڵە لە ئاڕاستەیەکدا ڕاستەھێڵێکی تر دروست دەبێت، دوو سەری ئەم دوو ڕاستەھێڵە بەیەک دەگەیەنین، چوارگۆشەیەک دروست دەبێت. ئینجا ئەم چوارگۆشە دەبەین لە بۆشاییەکی سێ ڕەھەندیدا و بەرەو سەرەوە ڕایدەکێشین، واتە بەرزی دەکەینەوە. شەشپاڵوویەک پێکدێت کە لە ناکۆتا چوارگۆشە دروست کراوە. ئەم شەشپاڵووە دەبەینە بۆشایی چوارڕەھەندی و لە ئاڕاستەیەکدا کە ئەستوونە لەسەر ڕەھەندەکانی تر ڕایدەکێشین، تێسێرەکتێک دروست دەبێت کە لە ناکۆتا شەشپاڵوو پێکھاتووە. [١]
وێناکردنی تێسێرەکت
[دەستکاری]وێناکردنی تێسێرەکت لە دونیای ڕاستەقینەدا کە سێ ڕەھەندییە، شتێکی مەحاڵە، لەبەر ئەوەی تێسێرەکت تەنێکی چوارڕەھەندییە. دەشێت مرۆڤ سێبەرێک لە تێسێرەکت وێنا بکات. لە ڕاستیدا ھەموو ھێڵەکانی تێسێرەکت ڕاستن و لە پێوانەدا یەکسانن و ھەموو گۆشەکانی وەستاون.
ھەڵوەشاندنەوەی تێسێرەکت
[دەستکاری]
لە ھەڵوەشاندنەوە یان ڕاخستنی شەشپاڵوویەک شێوەیەکی دوو ڕەھەندی دروست دەبێت (دەشێت لەسەر کاغەزێک بکێشرێتەوە) کە لە شەش چوارگۆشە پێکدێت، ھەروەھا تێسێرەکتێکی ھەڵوەشاو لە ھەشت شەشپاڵوو پێکدێت و شێوەیەکی سێ ڕەھەندییە .[٢]
پەراوێزەکان
[دەستکاری]- ^ Bowen، J. P. (April 1982). «Hypercubes». Practical Computing. ٥ (٤): ٩٧–٩٩. لە ڕەسەنەکە لە ٣٠ی حوزەیرانی ٢٠٠٨ ئەرشیڤ کراوە.
{{cite journal}}: نرخەکانی ڕێکەوت بپشکنە لە:|ڕێکەوت=(یارمەتی) «وەشانی ئەرشیڤکراو». لە ڕەسەنەکە لە ٣٠ی حوزەیرانی ٢٠٠٨ ئەرشیڤ کراوە. لە ٢٦ی ئازاری ٢٠١٨ ھێنراوە. - ^ «Unfolding an 8-cell». لە ڕەسەنەکە لە ٢٥ی تەممووزی ٢٠١٨ ئەرشیڤ کراوە. لە ٢٠ی تەممووزی ٢٠١٨ ھێنراوە.
سەرچاوەکان
[دەستکاری]- بەشداربووانی ویکیپیدیا، «تسرکت»، ویکیپیدیای فارسی. سەردان لە ٢٦ی ئازاری ٢٠١٨.
 | ئەم «ئەندازە» وتارە کۆلکەیەکە. دەتوانیت بە فراوانکردنی یارمەتیی ویکیپیدیا بدەیت. |
