پەڕگە:Kerr-surfaces.png
ڕواڵەت
Kerr-surfaces.png (٨٠٠ × ٥٨٨ پیکسڵ، قەبارەی پەڕگە: ٦٠ کیلۆبایت، جۆری ئێم ئای ئێم ئی: image/png)
مێژووی پەڕگە
کرتە بکە لەسەر یەکێک لە ڕێکەوت/کاتەکان بۆ بینینی پەڕگەکە بەو شێوەی لەو کاتەدا بووە.
| ڕێکەوت/کات | ھێما | ئەندازە | بەکارھێنەر | تێبینی | |
|---|---|---|---|---|---|
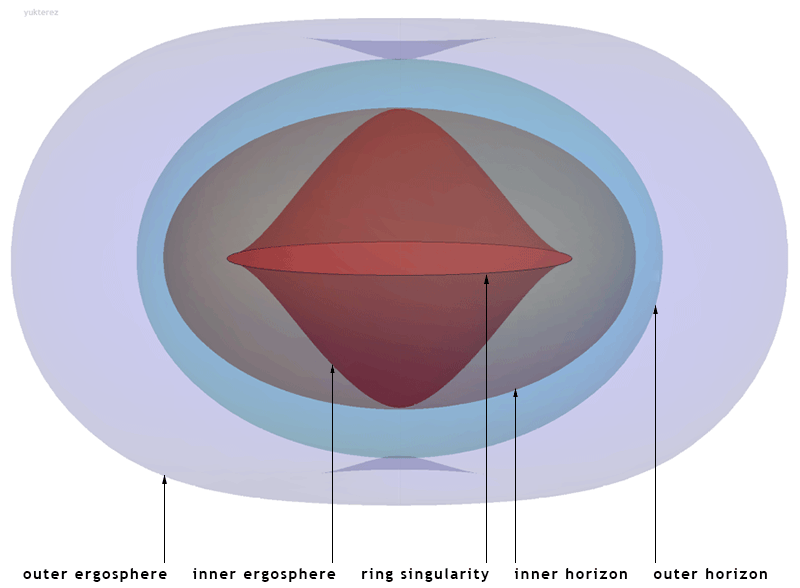
| هەنووکە | ٠٢:٤٨، ٢٩ی ئابی ٢٠٢١ |  | ٨٠٠ لە ٥٨٨ (٦٠ کیلۆبایت) | Yukterez | pointing the arrows to the outer edges of the surfaces to avoid 2D/3D confusions |
| ٠٥:٢١، ٢٥ی حوزەیرانی ٢٠١٧ |  | ٨٠٠ لە ٥٨٨ (٦٠ کیلۆبایت) | Yukterez | User created page with UploadWizard |
بەکارھێنانی پەڕگە
ھیچ پەڕەیەک نییە کە ئەم پەڕگەیە بەکاربھێنێت.
بەکارھێنانی سەرانسەریی پەڕگە
ئەم ویکیانەی دیکەی خوارەوەش ئەم پەڕگە بەکاردێنن:
- بەکارھێنان لە ar.wikipedia.org
- بەکارھێنان لە ca.wikipedia.org
- بەکارھێنان لە de.wikipedia.org
- بەکارھێنان لە en.wikipedia.org
- بەکارھێنان لە es.wikipedia.org
- بەکارھێنان لە eu.wikipedia.org
- بەکارھێنان لە fr.wikipedia.org
- بەکارھێنان لە fr.wiktionary.org
- بەکارھێنان لە it.wikipedia.org
- بەکارھێنان لە uk.wikipedia.org